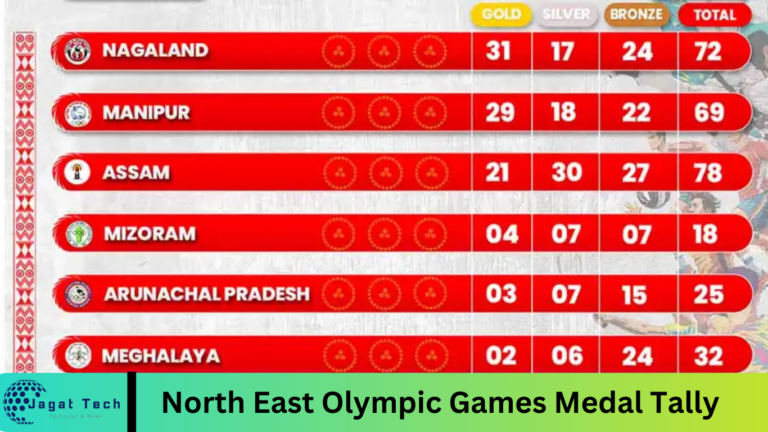
Selina Class 9 Maths Solution

Mastering mathematics can be challenging, but with the Selina Class 9 Maths Solution, students can streamline their learning process and achieve academic success. Selina Publishers offer meticulously curated textbooks and solutions that adhere to the ICSE syllabus, providing comprehensive guidance. This article dives into detailed solutions for Class 9 mathematics, helping students grasp concepts effectively and excel in exams.
Why Selina Class 9 Maths Solutions Are Essential
Selina Maths Solutions are indispensable for Class 9 students due to their structured, easy-to-follow approach. The solutions cater to the ICSE curriculum and are designed by experienced educators, ensuring clarity and precision. Key benefits include:
- Comprehensive Coverage: Every chapter and topic in the syllabus is thoroughly addressed.
- Step-by-Step Explanations: Detailed solutions enhance understanding and problem-solving skills.
- Exam-Focused Approach: Solutions align with ICSE exam patterns, aiding in effective preparation.
Chapter-Wise Breakdown of Selina Class 9 Maths Solutions
Selina Class 9 Maths Solutions
Chapter 1: Rational and Irrational Numbers
This chapter introduces the foundational concepts of rational and irrational numbers. Students learn about:
- Properties of rational numbers
- Representation of irrational numbers on the number line
- Simplifying complex expressions involving surds
Example Problem: Simplify 8+18\sqrt{8} + \sqrt{18}.
Solution:
8+18=22+32=52\sqrt{8} + \sqrt{18} = 2\sqrt{2} + 3\sqrt{2} = 5\sqrt{2}
Chapter 2: Compound Interest (Without Using Formula)
Understanding the principle of compound interest is crucial for financial mathematics. This chapter explores:
- Calculating compound interest through successive additions
- Real-life applications of compound interest
- Comparing simple and compound interest for given scenarios
Example Problem: Find the compound interest on ₹10,000 for 2 years at 5% per annum.
Solution: Successive calculations yield ₹1025.
Chapter 3: Expansions
This chapter focuses on polynomial expansions and algebraic identities. Key areas include:
- (a+b)2,(a−b)2,(a+b)3(a + b)^2, (a – b)^2, (a + b)^3 identities
- Solving real-life problems using expansions
- Factorizing complex polynomials using identities
Example Problem: Expand (x+2)3(x + 2)^3.
Solution:
(x+2)3=x3+3×2(2)+3x(22)+23=x3+6×2+12x+8(x + 2)^3 = x^3 + 3x^2(2) + 3x(2^2) + 2^3 = x^3 + 6x^2 + 12x + 8
Chapter 4: Factorization

Factorization simplifies algebraic expressions and equations. This chapter provides techniques such as:
- Grouping terms for factorization
- Using identities to factorize higher-degree polynomials
- Solving quadratic equations through factorization
Example Problem: Factorize x2+5x+6x^2 + 5x + 6.
Solution:
x2+5x+6=(x+2)(x+3)x^2 + 5x + 6 = (x + 2)(x + 3)
Chapter 5: Simultaneous Linear Equations
Students learn methods to solve linear equations, including:
- Substitution method
- Elimination method
- Cross-multiplication for two-variable equations
Example Problem: Solve 2x+y=72x + y = 7 and x−y=1x – y = 1.
Solution: Solving yields x=2,y=3x = 2, y = 3.
Chapter 6: Quadratic Equations
Quadratic equations are pivotal in algebra. This chapter teaches:
- Solving quadratic equations using the factorization method
- Applying the quadratic formula
- Analyzing roots through discriminants
Example Problem: Solve x2−5x+6=0x^2 – 5x + 6 = 0.
Solution: Roots are x=2x = 2 and x=3x = 3.
Chapter 7: Ratio and Proportion
This chapter simplifies real-world problems through ratio and proportion concepts, including:
- Direct and inverse proportions
- Applications in scaling and financial calculations
- Solving problems using cross-multiplication
Example Problem: If x:y=3:5x : y = 3 : 5 and y:z=2:7y : z = 2 : 7, find x:y:zx : y : z.
Solution: The ratio is 6:10:356 : 10 : 35.
Chapter 8: Trigonometry
Trigonometry is essential for understanding angles and dimensions. This chapter includes:
- Basic trigonometric ratios and identities
- Solving right-angle triangles
- Real-life applications of trigonometry in construction and navigation
Example Problem: Find sin30∘+cos60∘\sin 30^\circ + \cos 60^\circ.
Solution: sin30∘+cos60∘=0.5+0.5=1\sin 30^\circ + \cos 60^\circ = 0.5 + 0.5 = 1.
Chapter 9: Coordinate Geometry

Coordinate geometry links algebra with geometric figures. Students study:
- Plotting points on the Cartesian plane
- Calculating distances between points
- Understanding slopes and equations of lines
Example Problem: Find the distance between points (1,2)(1, 2) and (4,6)(4, 6).
Solution: Distance =(4−1)2+(6−2)2=5= \sqrt{(4 – 1)^2 + (6 – 2)^2} = 5.
Chapter 10: Triangles
Triangles form the foundation of geometry, and this chapter delves deep into:
- Properties of triangles
- Criteria for congruence: SSS, SAS, ASA, and RHS
- Applications of Pythagoras theorem in real-life scenarios
Example Problem: Prove that triangles with sides 5 cm,12 cm,13 cm5 \, \text{cm}, 12 \, \text{cm}, 13 \, \text{cm} form a right triangle.
Solution: Using a2+b2=c2a^2 + b^2 = c^2, verify 52+122=1325^2 + 12^2 = 13^2.
Chapter 11: Mensuration
Mensuration focuses on calculating areas and volumes, covering:
- Surface area and volume of cylinders, cones, and spheres
- Real-life applications in calculating material costs
- Advanced problems involving frustums of cones
Example Problem: Find the volume of a cone with a radius of 3 cm3 \, \text{cm} and height 4 cm4 \, \text{cm}.
Solution: Volume =13πr2h=13π(3)2(4)=12π cm3= \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi (3)^2 (4) = 12\pi \, \text{cm}^3.
Chapter 12: Statistics
Statistics teaches students how to organize and interpret data effectively. Key topics include:
- Drawing frequency distributions
- Calculating mean, median, and mode
- Applying statistical methods to solve practical problems
Example Problem: Find the mean of the data set: 10,15,20,25,3010, 15, 20, 25, 30.
Solution: Mean =Sum of observationsNumber of observations=1005=20= \frac{\text{Sum of observations}}{\text{Number of observations}} = \frac{100}{5} = 20.
Chapter 13: Probability
Probability introduces students to predicting outcomes mathematically. This chapter covers:
- Basic probability concepts
- Theoretical versus experimental probability
- Applications in daily life, such as games and predictions
Example Problem: What is the probability of drawing a king from a standard deck of cards?
Solution: Probability =Favorable outcomesTotal outcomes=452=113= \frac{\text{Favorable outcomes}}{\text{Total outcomes}} = \frac{4}{52} = \frac{1}{13}.
Chapter 14: Circles
Circles form a significant part of the geometry syllabus, and this chapter emphasizes:
- Properties of chords and tangents
- Theorems related to angles in a circle
- Applications of the cyclic quadrilateral theorem
Example Problem: Prove that the angle subtended by a diameter at the circumference is 90∘90^\circ.
Solution: Use the angle subtended by a semicircle theorem to validate the result.
Chapter 15: Construction
This chapter equips students with practical skills to construct geometrical figures. Key learnings include:
- Constructing bisectors of angles and segments
- Drawing tangents to circles
- Constructing triangles with given parameters
Example Problem: Construct a triangle given its base, altitude, and one base angle.
Solution: Step-by-step procedures guide students through the construction using a compass and ruler.
Chapter 16: Distance Formula
The distance formula bridges algebra and geometry, helping solve problems involving:
- Lengths of line segments
- Verification of collinearity of points
- Application to real-life scenarios like mapping and design
Example Problem: Verify if points (2,3)(2, 3), (4,5)(4, 5), and (6,7)(6, 7) are collinear.
Solution: Calculate pairwise distances and confirm if their sum equals the total distance.
Chapter 17: Coordinate Geometry
Coordinate Geometry is a blend of algebra and geometry, emphasizing the use of graphs and equations. Key concepts include:
- Plotting points on the Cartesian plane
- Deriving equations of straight lines
- Finding the slope of a line
Example Problem: Find the equation of a line passing through the point (3,−2)(3, -2) with a slope of 44.
Solution: Using the slope-intercept form y−y1=m(x−x1)y – y_1 = m(x – x_1), the equation is y+2=4(x−3)y + 2 = 4(x – 3), which simplifies to y=4x−14y = 4x – 14.
See also; Total History And Civics Class 10 Solution
Chapter 18: Graphical Representation
Graphs play a crucial role in visually interpreting data. This chapter guides students through:
- Plotting linear equations
- Understanding the significance of intercepts
- Solving simultaneous equations graphically
Example Problem: Solve the equations 2x+y=52x + y = 5 and x−y=1x – y = 1 graphically.
Solution: Plot each equation on a graph, and the intersection point represents the solution: x=2,y=1x = 2, y = 1.
Chapter 19: Inequalities

Inequalities extend algebraic skills by introducing concepts such as:
- Linear inequalities in one and two variables
- Graphical representation of inequalities
- Solving real-life problems involving constraints
Example Problem: Represent 2x+3y≤62x + 3y \leq 6 on a graph.
Solution: Shade the region satisfying the inequality below the line 2x+3y=62x + 3y = 6.
Chapter 20: Mathematical Reasoning
This chapter sharpens logical thinking by introducing:
- Statements and their negations
- Understanding implications and equivalence
- Solving problems using truth tables
Example Problem: Determine if the statement “If x>3x > 3, then x2>9x^2 > 9” is true.
Solution: Verify for x=4x = 4, true; verify for x=2x = 2, false.
Tips for Maximizing Results Using Selina Class 9 Maths Solutions
- Practice Regularly: Repeated practice enhances problem-solving speed and accuracy.
- Focus on Weak Areas: Allocate more time to challenging chapters.
- Revise Key Concepts: Regular revision reinforces learning.
FAQs on Selina Class 9 Maths Solution
What is the Selina Class 9 Maths Solution?
The Selina Class 9 Maths Solution is a comprehensive guide offering step-by-step solutions to all exercises in the Selina ICSE Mathematics textbook for Class 9. It helps students understand concepts clearly and solve problems efficiently.
Is the Selina Maths Solution aligned with the ICSE syllabus?
Yes, the Selina Maths Solution strictly follows the ICSE syllabus, ensuring that all solutions are relevant and accurate for Class 9 examinations.
Can Selina Maths Solutions help me score higher marks in exams?
Absolutely. The solutions provide detailed explanations and solve problems systematically, helping students build confidence and improve their performance in exams.
Are the Selina solutions suitable for self-study?
Yes, the Selina solutions are designed for self-study. The step-by-step explanations make it easy for students to learn and practice independently.
How do I use the Selina Maths Solution effectively?
To use the Selina Maths Solution effectively:
Study one chapter at a time.
Practice solved examples before attempting exercises.
Use the solutions to verify your answers and identify mistakes.
Revise frequently to retain concepts.
Does the Selina Maths Solution include real-life applications?
Yes, the solutions include practical examples and application-based problems, helping students understand how mathematical concepts apply to real-world scenarios.
Conclusion
The Selina Class 9 Maths Solution is a valuable resource for ICSE students. Its well-structured approach ensures thorough understanding and effective exam preparation. With detailed explanations and a focus on core mathematical concepts, Selina solutions empower students to excel in their academic journey.